Lineaire regressie.

Wil je naar verbanden kijken tussen twee scale variabelen dan maak je gebruik van de lineaire regressie techniek. Verbanden tussen twee scale variabelen worden weergegeven door de correlatie coëfficiënt R. R is een waarde tussen +1 en -1. Naarmate R dichter bij de +1 ligt is er sprake van een positief verband, naarmate de R dichter bij de -1 ligt, een negatief verband en naarmate de R dicht bij 0 ligt geen verband.

Laten we kijken of er een verband is tussen de leeftijd en het inkomen. Bij leeftijd en inkomen is leeftijd de onafhankelijke variabele die het inkomen (de afhankelijke) bepaalt.

Heb je de "Analysis Toolpak" (hoe dit Toolpak installeert zie je in "Installeren Toolpak") geïnstalleerd dan vind je onder het tabblad "Gegevens" "Gegevens analyse".

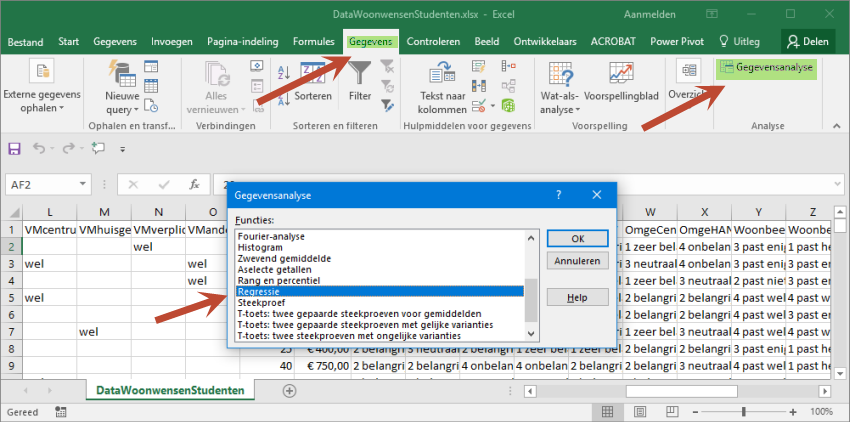
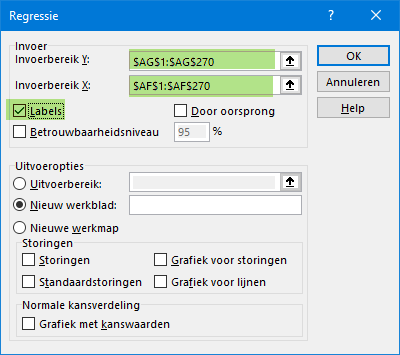
Selecteer "Regressie" en klik op "OK". Selecteer de gebieden. De kolom van het "Inkomen" plaats je onder "Invoerbereik Y:" (afhankelijke variabele) en de "Leeftijd" onder "Invoerbereik X:".
Als je de kolom titels meeneemt, zoals ik gedaan hebt, klik je "Labels"aan.

Je krijgt de volgende uitvoer:

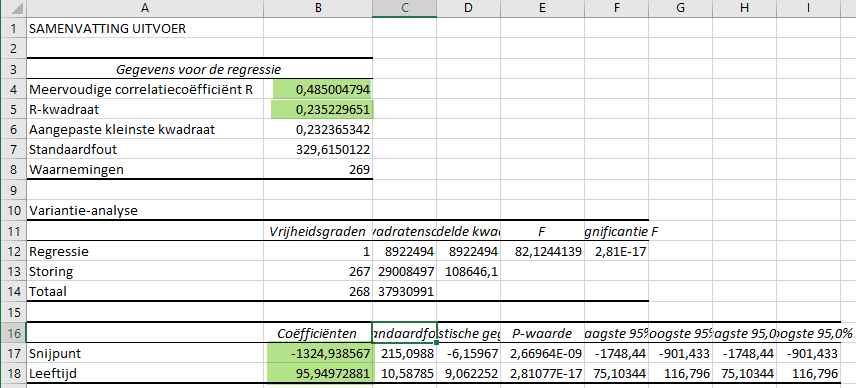
De Correlatiecoëfficiënt R is 0,49 afgerond. Dit is vrij laag. Er is dus bijna geen samenhang. Dit kun je ook zien aan de R-kwadraat. Deze is 0,24. Dat wil zeggen dat het inkomen maar voor 24% (0,24) verklaard wordt door de leeftijd bij deze groep studenten.

Het bij leeftijd en inkomen behorende spreidingsdiagram ziet er als volgt uit:

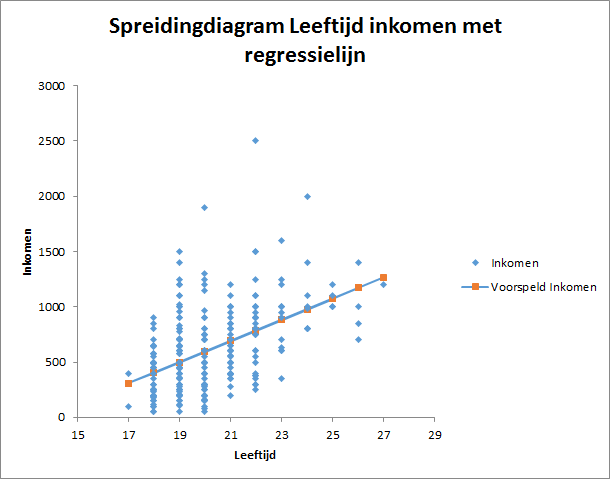
Hoe je een spreidingsdiagram kunt maken zie je in "Spreidingsdiagram maken".
In het spreidingsdiagram zie je de regressielijn van het voorspelde inkomen. Een lijn heeft een vergelijking meestal voorgesteld door : Y=aX +b, waarbij X de onafhankelijke variabele is, Y de afhankelijke, a de richtingscoëfficiënt van de lijn en b het snijpunt met de Y-as.
De samenvatting uitvoer geeft de waarden a en b.

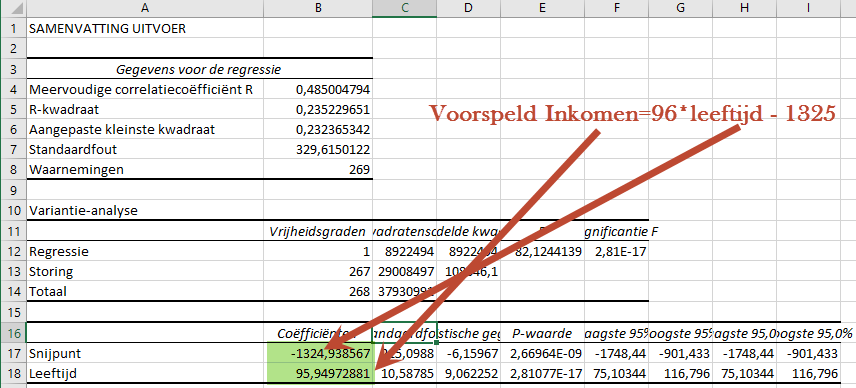
De vergelijking van de regressielijn: Voorspeld Inkomen=96*leeftijd - 1325.