Chi-kwadraattoets twee variabelen.

Om te toetsen of er verschil is in de uitkomsten van waarden van twee variabelen met een kwalitatief meetniveau (Nominaal of ordinaal) wordt de Chi-kwadraattoets gebruikt.

De Chi-kwadraat toets wordt toegepast op een draaitabel.

Voorbeeld 1.

Stel we willen weten of de verdeling van mannen en vrouwen per opleiding gelijk is. Dan onderzoeken we dat door de volgende stappen te nemen.

Maak als eerste een draaitabel om te zien of er daadwerkelijk verschil is in aantal mannen en vrouwen per opleiding.

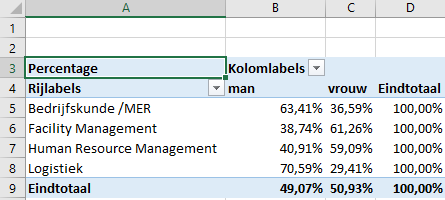
De percentages moeten rij percentages zijn.
In de tabel zien we dat er bij logistiek 71% mannen en 29% vrouwen zijn, terwijl bij Human Resource Management 41% mannen en 59% vrouwen. Dit is zeker niet gelijk. We gaan dit toetsen met de volgende hypotheses:

H0 : De verdeling van mannen en vrouwen over de opleidingen is gelijk.
H1 : De verdeling van mannen en vrouwen over de opleidingen is niet gelijk.

Het toetsen gaat volgens de volgende stappen.

Maak eerst of pas de percentage tabel aan in een draaitabel waarin de aantallen staan.

 

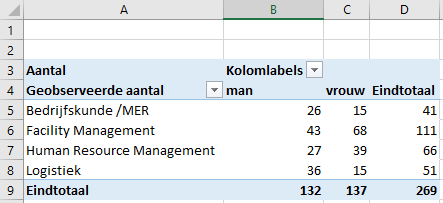
Kopieer en plak de tabel met plakken speciaal

Verwijder daarna de cellen waarin de aantallen staan, en voeg een rij (rij 18) in waarin onderstaande formules staan. Als je de formules ingevuld hebt moeten er de waarden komen te staan die nu in de rij eronder staan.

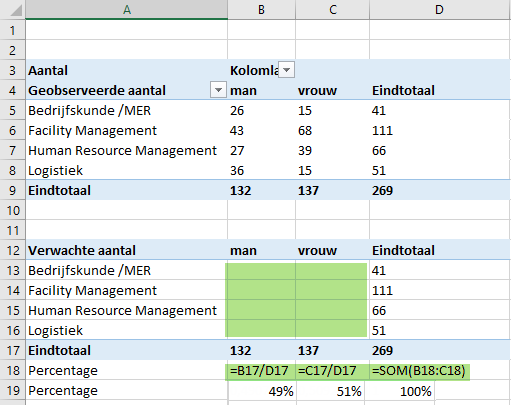
Uitleg: De bovenste tabel geeft aan de geobserveerde waarden van de enquête. In de onderste tabel willen we de verwachte waarden weergeven. Ervan uitgaande dat er geen verschil is verwachte aantallen mannen en vrouwen per opleiding zouden de verwachte aantallen per opleiding gelijk moeten zijn aan de verhouding van het totaal aantal mannen en vrouwen. Het percentage mannen is dan gelijk aan 132/269 is 49% en het percentage vrouwen is gelijk aan 137/269 is 51 %.

De verwachte aantallen mannen voor de opleiding MER zou dan moeten zijn 49% van 41, voor FM 49% van 111 enz. Ga na dat je dan de volgende formules moet invullen in het gebied B13:C16.

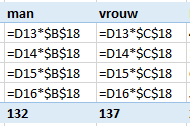
Met het volgende resultaat:

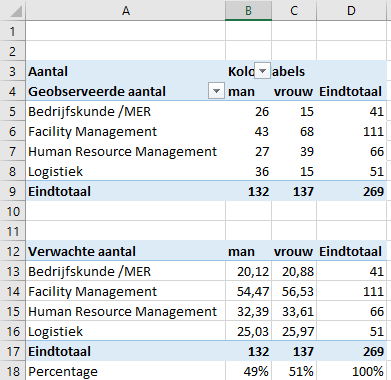
Rond deze getallen niet af.

Voer in Rij 20 de labels en de formule van de Chi kwadraat toets als volgt in:

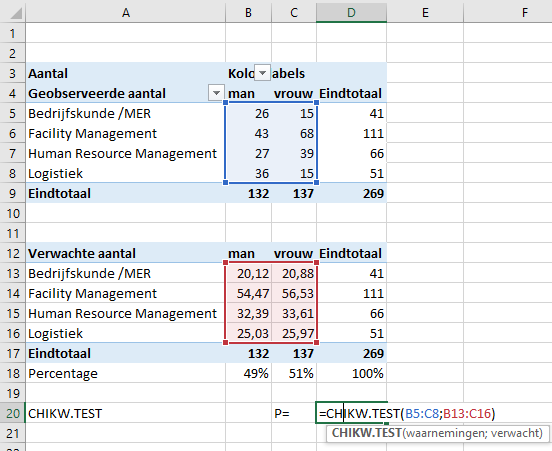
Dit levert een P waarde op van 0,00023425. Deze waarde is kleiner dan 0,05 dus we verwerpen de H0 hypothese. Er is dus een significant verschil in de verhouding mannen vrouwen per opleiding.

 

Voorbeeld 2

In de enquête zijn foto's en beschrijvingen van woningen bevraagd. Bij woonbeeld 2 valt bij een eerste onderzoek op dat er een verschil is in de keuzes per opleiding. We gaan onderzoeken of dit verschil significant is.
H0 : Er is geen verschil in keuzes bij woonbeeld twee tussen de opleidingen.
H1 : Er is wel een verschil in keuzes bij woonbeeld twee tussen de opleidingen.

De eerste stap is een draaitabel maken: Maak onderstaande tabel. De percentages moeten kolompercentages zijn. Ga na!

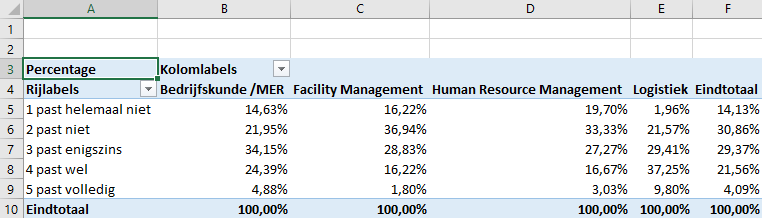
Verander de waarden in de tabel van percentages naar aantallen. (Handig is om voordat je dat gedaan hebt de laatste kolom met het "Eindtotaal" te kopiëren en met plakken speciaal waarden in G13:G19 te plaatsen).
Kopieer daarna de tabel (A4:F10) en plak de hele tabel met plakken speciaal, waarden, naar A13.
Verwijder daarna de waarden in het gebied B14:E18. Je krijgt onderstaand figuur.

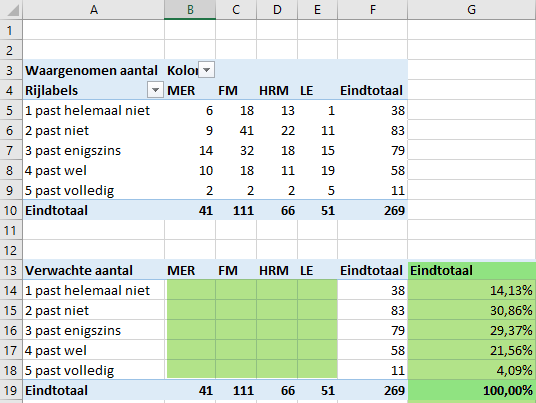
Voer de volgende formules in in B14:E18

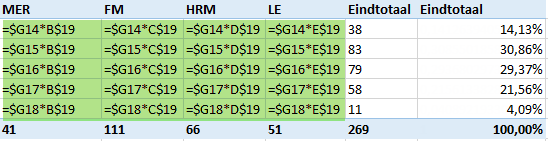
En bereken de CHIKW.TEST

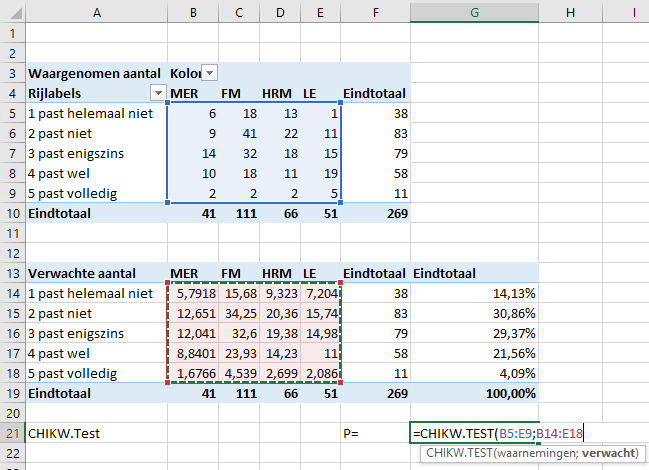
De p waarde is 0,012904 is kleiner dan 5% dus er is een significant verschil in woonbeeld 2 per opleiding.