Pearson PM toets.

De Pearson PM toets wordt gebruikt om te toetsen of de geconstateerde samenhang tussen twee scale variabelen wel of niet van het toeval afhangt. Om te kijken of er en hoe groot de verbanden zijn tussen twee variabelen gebruiken we Lineaire Regressie. Voor uitleg van de hieronder gebruikte functies zie daarvoor het onderdeel Lineaire Regressie. In dat onderdeel hebben we al gezien dat in de gebruikte dataset weinig sprake is van echt verband. De variabelen waartussen het meeste verband was waren leeftijd en inkomen, ook al was dit verband niet groot. In voorbeeld 1 zullen we de Pearson PM toets voor het verband tussen leeftijd en inkomen bespreken, voor voorbeeld 2 nemen we een voorbeeld waar wel meer verband tussen de varaiabelen is, maar waarvan de data niet in de gebruikte dataset zit.

Voorbeeld 1

We bekijken het verband tussen Leeftijd (onafhankelijke, x) en inkomen (afhankelijke, Y).

Het spreidingsdiagram is

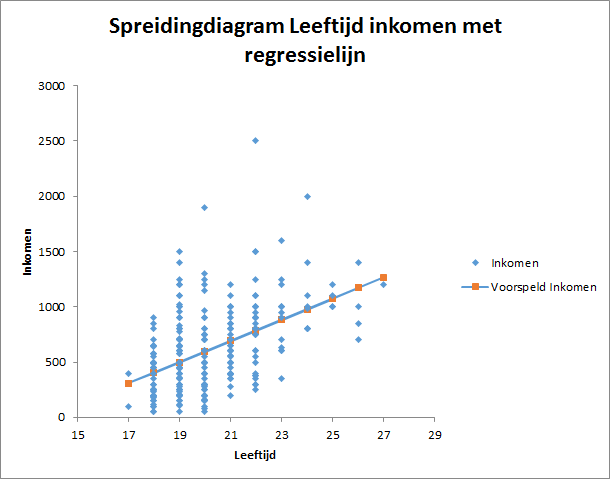
Uit beiden zien we al dat het verband niet erg groot is.

Kopieer leeftijd en inkomen naar een apart werkblad.
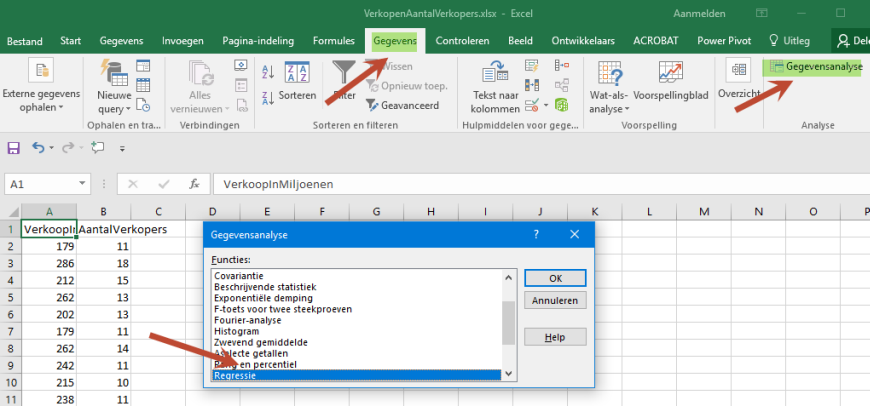
kies daarna uit het tabblad "Gegevens" voor "gegevensanalyse" .

Kies binnen gegevensanalyse voor Regressie.

Het inkomen is de afhankelijke variabele (invoerbereik Y), de leeftijd de onafhankelijke (invoerbereik X). Klik de labels aan en zorg dat de uitvoer in D1 geplaatst wordt en klik op "OK".

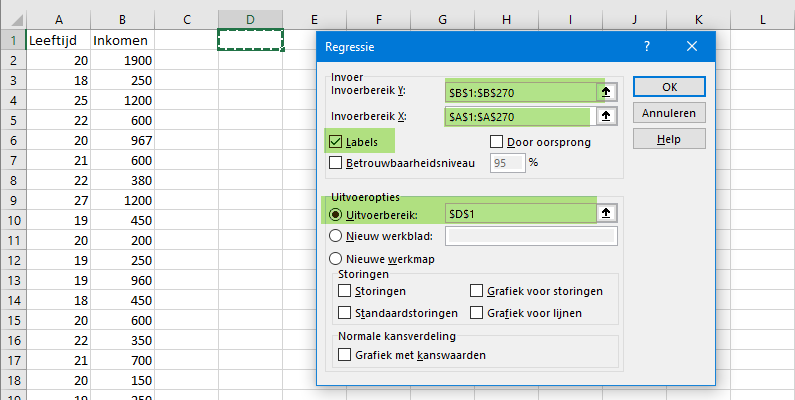
Je krijgt de volgende output.

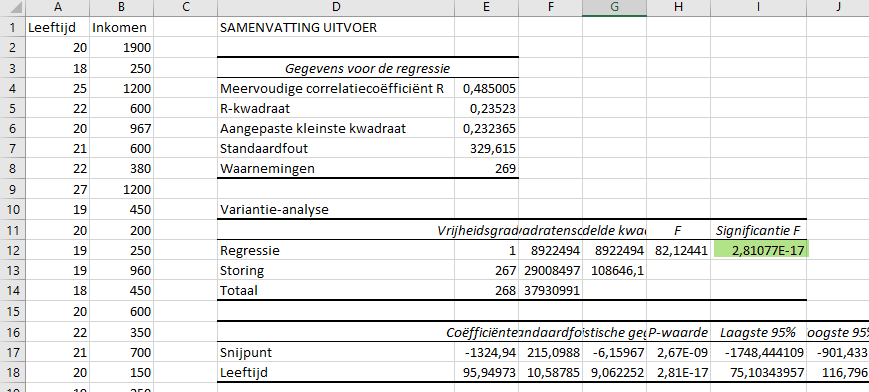
Voor de uitleg van de meeste onderdelen zie het onderdeel "Lineaire Regressie".
Voor het toetsen is van belang de waarde onder "Significantie F". Dit is n.l de P waarde.

De P waarde hier is 2,81077 E-17.

Stel we hebben de volgende hypothesen:
H0: er is geen verband tussen de leeftijd en het inkomen.
H1: er is wel verband tussen de leeftijd en het inkomen.

De correlatiecoëfficiënt is 0,485005. Dit is een matig verband en omdat de P waarde kleiner is dan 0,05 is het verband significant.

Voorbeeld 2

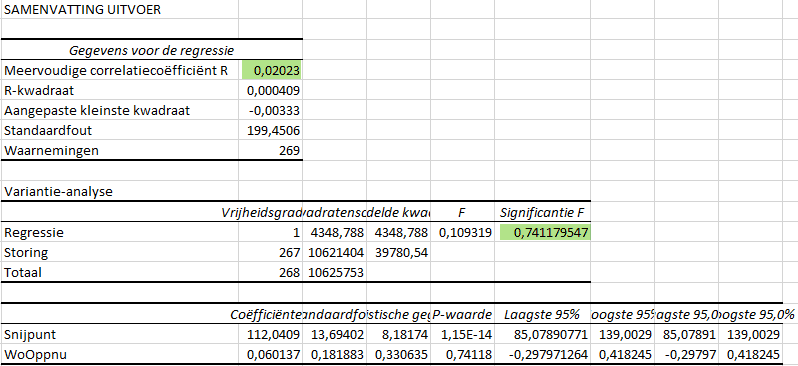
Zouden we kijken naar het verband tussen woonoppervlakte en woonlast, dan zien we dat de correlatiecoëfficiënt 0,02 is (heel erg klein) maar ook dat het significantieniveau 74% is. M.a.w. verband is er niet, en is ook niet significant.

Voorbeeld 3

Voor dit voorbeeld gebruiken we het volgende bestand "VerkopenAantalVerkopers.xlsx". Download dit bestand en open het.
Om inzicht te krijgen in de relatie tussen het aantal verkopers (Onafhankelijke, x) en de verkopen in miljoenen (afhankelijke, y) voeren we de regressieanalyse uit.

De Verkopen in miljoenen is de afhankelijke variabele en het aantal verkopers de onafhankelijke.

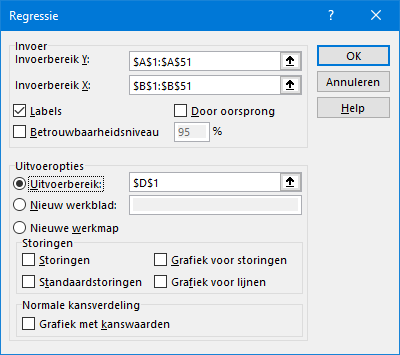
met als resultaat:

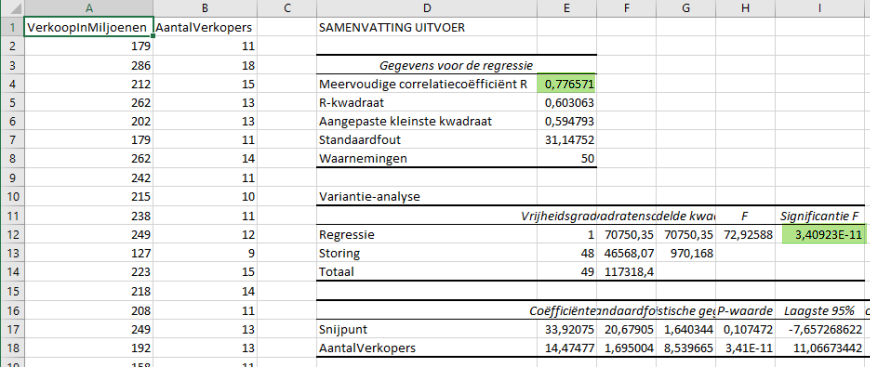
De correlatiecoëfficiënt is groter dan 0,7, dus er een redelijk verband. Uit de R kwadraat is af te lezen dat de verkopen voor 60,3% verklaard worden door het aantal verkopers.
De p waarde is 3,40923E-11 is kleiner dan 0,05. Er is dus een significant positief verband tussen het aantal verkopers en de verkopen.